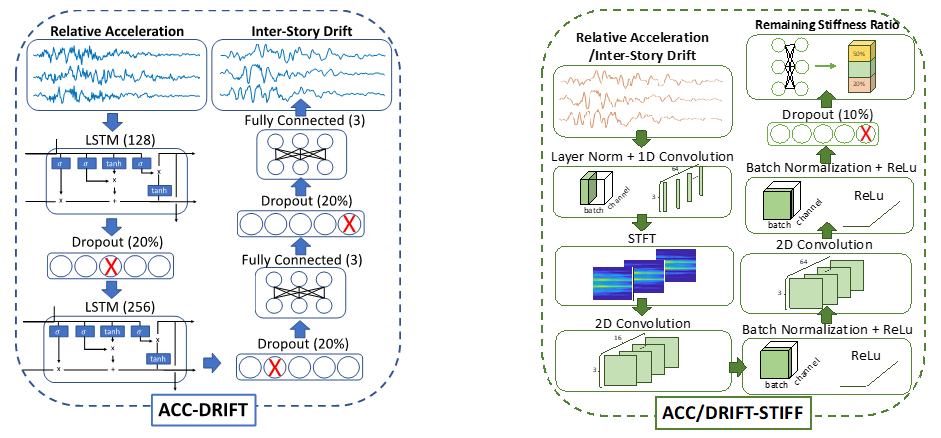
現行建築結構設計規範是採層間位移作為結構損壞指標,即當樓層結構位移達0.2%至0.4%,此時結構進入非線性行為,並造成部分構件損壞。此外,過去研究指出結構勁度變化時,結構自然頻率改變,如頻率響應函數之極點位置。在本研究中,研發兩種多目標神經網路模型,目的是透過樓層加速度反應,同時預測各樓層層間位移及殘餘勁度比。第一種方法採用基於物理含義之損失函數作為目標函數的並聯式模型,而另一種方法結合神經網路與遷移學習成整合式學習模型。針對層間位移估計中,引入雙長短期記憶層之學習模型,可由樓層加速度量測,轉化為位移,如圖一所示;在預測殘餘勁度比中,加入短時傅立葉層,在輸入序列中加入二維卷積層,獲取頻域上重要特徵進行模型訓練,如圖二所示。數值結果顯示,採用物理含義損失函數之多目標模型(見圖三),其在殘餘勁度比的預測精度上,與單目標模型及採MSE損失函數(Mean squared error loss function)之多目標模型相當,而在真實層間位移之相關係數則高於其他二種方法,意謂採物理含義損失函數之多目標模型中,可於層間位移預測上具高精度表現。另一方面,整合式學習模型(見圖四)透過遷移學習的概念,首先針對真實層間位移與真實殘餘勁度比產生一子模型,同時以各樓層加速度與層間位移產生另一子模型,在結合兩子模型中透過全連接層與權重微調達到更快速的收斂效果,亦改善單目標模型引致的誤差累積,提高殘餘勁度比估計精度。最後透過足尺結構的結果顯示,兩模型在預測層間位移及殘餘勁度比上與實際皆達一定相關趨勢,尤以採物理含義損失函數之多目標模型更為準確。綜合本研究結果,無論是採物理含義損失函數之多目標神經網路,抑或基於遷移學習概念之整合式學習神經網路,皆可有效達到樓層層間位移及殘餘勁度比之多目標預測。(土木系張家銘教授提供)

圖三 採物理含義損失函數之並聯式多目標模型

圖四 基於遷移學習之整合式模型