本研究團隊對於平台式和自走式二維壓電致動器的研究已有多項技術開發,驅動方法包括整數倍頻驅動、雙模態驅動及整數倍頻雙模態驅動等三種方法,其中整數倍頻雙模態驅動(Two-Integer-Frequency Two-Mode, TIF-TM)驅動方法,是為目前效率最高之驅動方法,然而目前之設計方法,尚未考慮空間相位之效應,並且對於驅動參數,皆是將其設計之結構進行數學建模,接著針對其結構及所需振形設計成本函數,再調變驅動參數觀察成本函數以間接的方式獲得最佳參數。本研究從波傳的角度出發,開發可將空間相位及時間相位一併進行分析方法,開發出可將兩驅動共振頻的時間及空間相位差皆驅動在 π/2 的位置,進而整合分析出產生高效行進波的條件,並開發可自動找尋驅動條件的設計流程。致動器由壓電材料和不鏽鋼結合的複合結構,並於 x 方向以簡支端作為邊界條件,y 方向以自由端作為邊界條件,如圖1。在整合了時間域與空間域相位後,本研究提出一函數 Cs3(x,t) 可以用來預測行徑波產生的位置,如圖2、3。可以看到產生行進波的位置也符合 Cs3(x,t) 圖的預測,由此可知此分析方法之可行性。不同於以往利用成本函數找出最佳參數解,本研究將生成行進波之條件進行驅動訊號設計。相位差方面除了相位差必須為π/2之外,若低模態的波腹與高模態的節點進行疊加能夠形成良好的行進波,驅動相位( θi )於變形解中的時間項內,且變形解中的時間項本身具有一個相位 Φi 如圖4,需消去其影響。圖5為頻率差2倍的弦波疊波示意圖,當高模態之波腹(P2)的振幅值加上低模態相對應位置(N1)的振幅值,相等於高模態之節點(N2)的振幅值加上低模態之波腹(P1)的振幅值,則可於高模態之兩波腹(P2)間獲得平緩的行進波,以達成最高行徑波效率,以此計算出最佳兩弦波電壓比。圖6~8為根據本研究得出之最佳行進波與其成本函數圖形。由此可知,透過本研究團隊提出的方法可以最佳化驅動方法。(工科海洋系李世光教授提供)
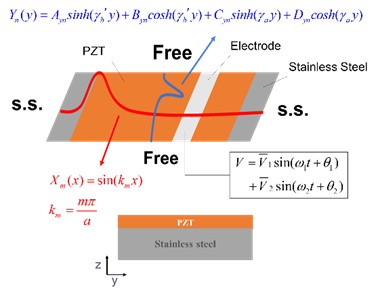
圖 1 2-D壓電制動器結構圖
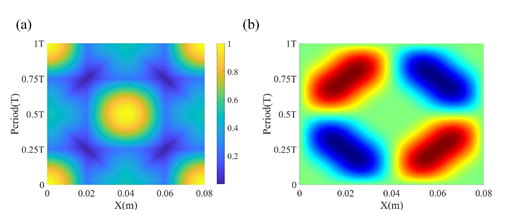
圖 2 Φ21及Φ41疊加產生之(a) Cs3 (x,t)圖與(b)時間域波型圖
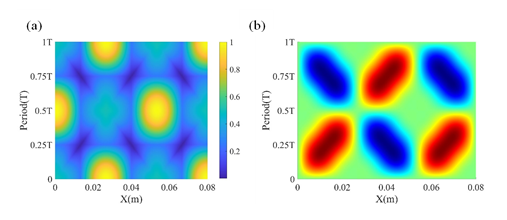
圖 3 Φ31及Φ61疊加產生之(a) Cs3(x,t)圖與(b)時間域波型圖
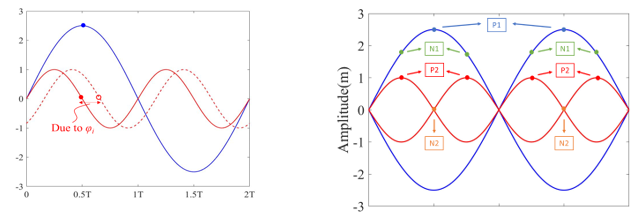
圖 4 時域之 Φi 造成相移示意圖 圖 5 電壓比設計示意圖
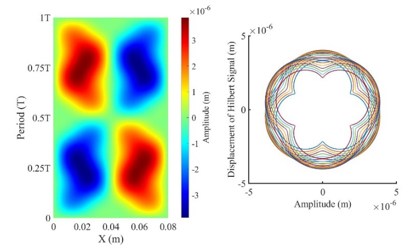
圖 6 S21/41 結構驅動之數值模擬所得波形圖與希爾伯特圓
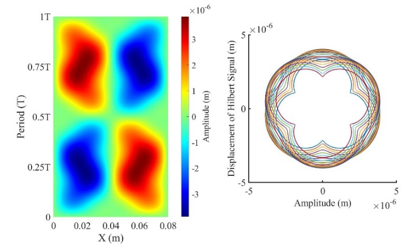
圖 7 S21/41 結構驅動之有限元素模擬所得波形圖與希爾伯特圓
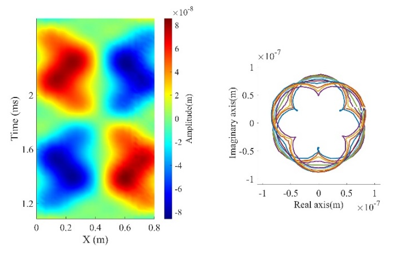
圖 8 S21/41 結構實驗輸入驅動訊號之時間域波形圖與解析訊號於複數平面作圖