濃密乾顆粒流常見於自然災害與工程應用,為了有更好的預測與製程設計,其運動方程式及求解廣受研究。此研究的挑戰在於離散的組成顆粒可聚集堆積表現像固體承受剪切力、也可激發後快速彈跳滾動形成類流體連續形變。近年頗為成功的局部μ(I)-流變定律(local rheology law)描述顆粒流剪切與正向應力的比值—有效摩擦係數(μ)—如何隨流體慣性數(I, inertial number)單調非線性地成長,將此流變律引入動量方程式、搭配合理邊界條件,能成功預測許多穩態快速顆粒流。
然近期文獻指出此局部模型無法完整描述慢速流動顆粒流或是其將止或起動的動態過程。此乃因局部模型並未考慮應力的遲滯現象,此現象與忽略顆粒內部因摩擦生成的力鏈結構(force chain structure)以及其跨顆粒尺度的傳遞效應有關。因此,本實驗室與其他團隊各自發展出各類複雜度與廣度不同的非局部μ(I)本固模型,得到一個具降伏強度的非牛頓流體運動模型,其非線性的特徵造就數值求解的必需。
為驗證與應用,本實驗室拓展計算流體力學方法,在Volume of Fluid (VOF)方法架構下建構對應的pressure implicit with splitting of operators(PISO)算則,並利用正規化的演算法(Regularization scheme)處理奇異點,完成文獻上第一個求解此類流體的CFD模擬,成功計算出許多實驗上觀察到的慢速濃密顆粒流特殊的動態現象。
本研究貢獻之一,是透過局部與非局部模性計算結果的比較,首度確認非局部效應確實是造成許多實驗上觀察到的慢速濃密顆粒流特殊動態現象的關鍵,也是現今文獻上首位可以捕捉shear banding的黏流計算;本研究貢獻之二,是進一步透過無因次分析與針對流變參數系統性的探討,找出非局部效應相依的無因次參數,能預測流況轉變,可作為未來應用面上是否需要引入非局部模型模擬的根據。(機械系楊馥菱教授提供)
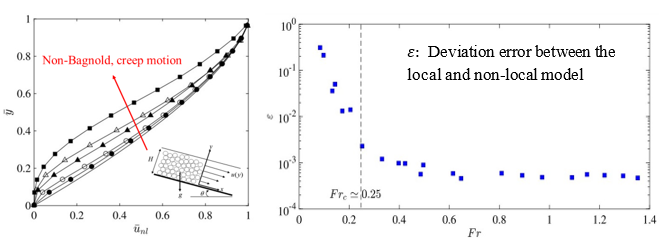
(左) 第一個透過CFD重現穩態斜坡流non-Bagnold 速度分布曲線、驗證了顆粒計算所發現的非局部現象; (右) 針對穩態斜坡流應用(多見於自然災害),發現福祿數(Froude number)低於0.25時需啟動非局部本固模型的計算,才能有較正確的流場預測
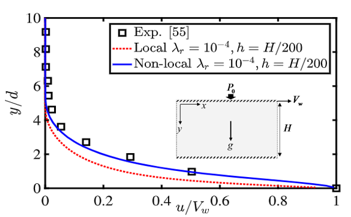
慢速剪切流需引入非局部本固模型的計算,才能重現實驗量測