The control of acoustic and elastic waves via engineered materials has several important real-world applications such as non-destructive evaluation of structural components, synthesis of biomedical devices, high-resolution imaging, and remote sensing. Being formulated as inverse problems, all these applications share as a common denominator the need for efficient solution methodologies. Available techniques, mostly based on conventional optimization approaches, have shown some significant limitations in terms of the ability to explore a vast design space and to limit the computation burden. In this study, a novel deep auto-encoder (DAE) based approach is proposed in order to solve a benchmark inverse problem consisting in designing assemblies of acoustic scattering elements capable of molding an incoming plane wave into a target (user-defined) downstream pressure distribution. The proposed approach is validated numerically through three design scenarios, involving either a single or multiple scatterer configuration, and target pressure fields defined at different frequencies, as shown in Figure 1. The proposed network, as shown in Figure 2, consists of a geometry estimator and a DAE that imposes constraints due to the physics of the problem on the geometry estimator during the learning process which leads to more robust design. By joint optimization, the estimation of scatterer geometry is strengthened with the latent representations of the target pressure field learned by the DAE. For a trained network, the design inference is quasi-instantaneous given a target 2D pressure field. The proposed approach achieves a 99.91% accuracy on the testing samples, and the required computation time during the design stage is reduced by a factor of 195 when compared with a baseline reference implemented using the genetic algorithm. Moreover, the generalization capability of the proposed network is further explored by using a dataset generated based on scatterers having new shapes. Lastly, a mathematical interpretation of the trained kernels is investigated in detail using the principle of convolution. (土木系吳日騰教授提供)

Figure 1. The amplitudes of the scattered pressure fields generated using a scatterer configuration with wave frequencies 200 (Hz), 796 (Hz), 5000 (Hz), and 12,500 (Hz). The objective is to design the geometry of the wave scatterers given a user-defined downstream pressure fields indicated with dashed lines.
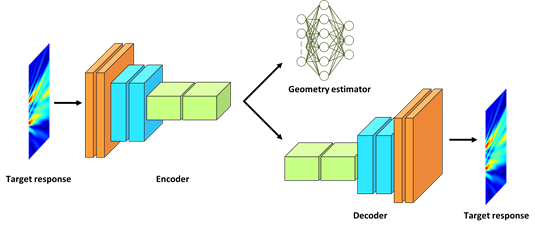
Figure 2. The proposed network architecture consists of a DAE and a geometry estimator that determines the shapes of the wave scatterers. By the joint training of the DAE and the geometry estimator, physics constraints are imposed to the training of the geometry estimator, leading to a more robust design.

Figure 3. An example of the input and output of the DAE: (a) Real and (c) imaginary parts of a sample network input, and the corresponding (b) reconstructed real and (d) reconstructed imaginary parts of the input pressure field. These visualizations are reported using one sample in the test dataset. (Unit: Pa)