Complex bioconvection patterns have been studied analytically, experimentally, and numerically previously only for a flat free-surface of a suspension of chemotaxis bacteria in a shallow/deep chamber. In this paper, we have considered a two-dimensional chemotaxisdiffusion-convection system with a deformed free-surface. The top of the chamber is open to the air, and the motion of the fluid in a rectangular chamber satisfies the tangential stress condition prescribed on the free-surface. The bottom and the side walls are rigid and impermeable to bacteria and oxygen (see Figure 1).The influence of aggregation of chemotactic cells on the deformed free-surface of a shallow chamber is studied analytically. The aim of this paper is to investigate the nature of the instability in the chemotaxis-diffusion-convection system. We performed a detailed linear stability analysis of a steady-state cell and oxygen concentration distribution. The system becomes dominated by nonlinear convection terms beyond a critical Rayleigh number Raτ, which also depends on the critical wavenumber k as well as the other parameters. We have investigated that how the critical Rayleigh number in this system varies with three different sets of parameters. A weakly nonlinear analysis is carried out as well to determine the relative stability of the pattern formation at the onset of instability. A reactance between rolls, squares, hexagons, and mixed mode pattern is investigated in detail. Further research should link the weakly nonlinear analysis with the bifurcation analysis. Some important direct numerical simulation results have been presented in the support of linear stability analysis. Comparison of the analytical steady-state solution shows good agreement with the numerical result. Numerical results of concentration of bacteria for Raτ = 120.6 at different stage are shown in Figure 2, and Figure 3 shows the velocity magnitude at different values of Rayleigh number, Raτ. (許文翰教授提供 twhsheu@ntu.edu.tw)
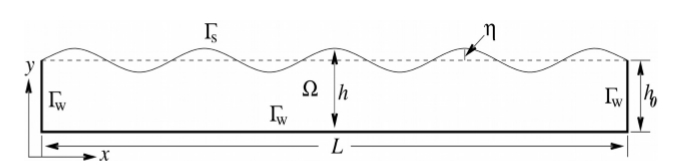
Figure 1. A schematic diagram of a two-dimensional chemotaxis system with the liquid-air interface Γs , where the oxygen concentration is equal to that of air, not crossed by bacteria. A no-slip boundary condition is imposed at the container walls Γw.
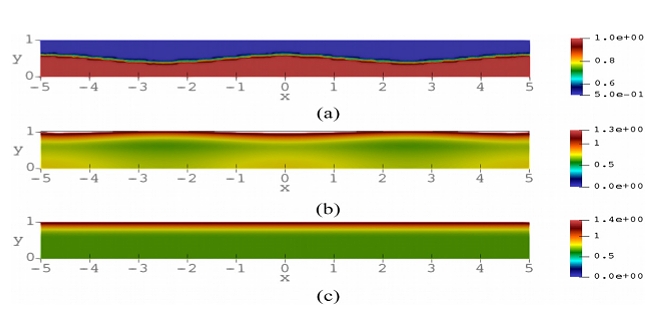
Figure 2. Bacteria concentration for the case with the Rayleigh number Raτ = 120.6, (a) t = 0.0, (b) t = 0.8, (c) t = 2.5.
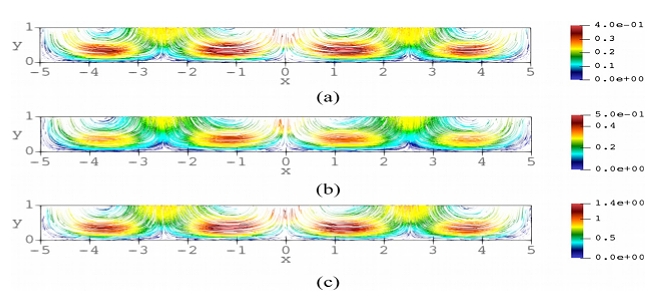
Figure 3. Velocity field (streamlines) at the beginning of the process for Rayleigh numbers: (a) Raτ = 115, (b) Raτ = 120.6, and (c) Raτ = 400.